信号之间的时延估计（续）

已置顶 | Posted on: | In: |
Words count in article: 6.7k字 | Reading time ≈ 26分钟

说明

这篇文章是之前《信号之间的时延估计》的续篇，中间隔了很长时间才写这一篇，是因为期间一直有其它事情要做，而且感觉对GCC的一些关键点还没有考虑清楚。后来评论区一位朋友在关心续篇的进度，我就不得不抓紧时间好好思考一下了哈哈。因此最终写了这一篇作为上一篇的修正以及补充。

PS：这篇文章内容较多，能把这么枯燥的内容看完也不容易。

1. 上一篇的错误

经过更加深入的思考后，这里首先指出，以前的一些“想当然”的看法明显是错误的。我在上一篇文档中关于GCC的理解部分写到：

其实，信号进行了PHAT加权后，实质上相当于进行了白化滤波，倘若信号转换为了理想的白噪声形式，则时域中必然会在零延时处出现冲激，这是由傅里叶变换决定的。然而仅进行了幅度上的归一化尚且不能认为是理想的白化，被保留的相位信息仍占据主导因素，因此会在准确的时延处产生更大的冲激。因此两路具有确定延时关系的信号在进行GCC-PHAT后会获得两个冲激峰值。如果两路信号不具备延时关系，则它们的相关性很小，因此进行PHAT加权而产生的频谱更加趋向于理想白噪声，因此它们的时域结果也趋向于在零时延处产生较大峰值。

这种说法是错误的，即便在频域进行了白化滤波，事实上也不会在0时延处产生同样的冲激。错误的原因在于，我将功率谱和自相关，以及频谱与时延这两对关系弄混了。

对一个信号进行分析时，首先应该明确该信号属于确定信号还是不确定信号（随机信号）。而噪声则比较特殊，一般将其作为随机信号并使用统计的规律来进行分析，此时噪声的功率谱和自相关是互为傅里叶变换的，并且对于白噪声而言，其功率谱是常数，此时的自相关函数会在0时延处产生一个冲激。而将其作为确定信号进行分析的时候，可以发现白噪声的频谱的成分十分混杂，反变换到时域也是十分混杂的噪声形式。

事实上，对于一个确定的信号的频谱，对幅度进行归一化确实是白化的一个步骤，但是不能等价于“白化”。此时该信号在时域能否产生冲激，是由信号相位谱之间的关系决定的。事实上，只有确定的线性相位才会在时域产生对应的冲激，这一点是由傅里叶变换决定的。即 ${exp(jwt_0)}$ 变换为 ${\delta(t-t_0)}$，当时延 ${t_0}$ 为常数的时候，频域上的复指数信号 ${exp(jwt_0)}$ 是典型的“幅度归一化+线性相位”的形式。

而对于几乎没有确定的线性相位的频谱形式，可以认为由很多个线性相位叠加而成，因此时域上也就会出现十分混杂的冲激，具体的理论推导见第二部分。

以下是直接从频域生成白噪声并观察其时域波形：

1
2
3
4
testSignal = ifft(exp(1i*pi*randn(1,1000)));
figure;
plot(real(testSignal));
title('白噪声频谱的时域波形');

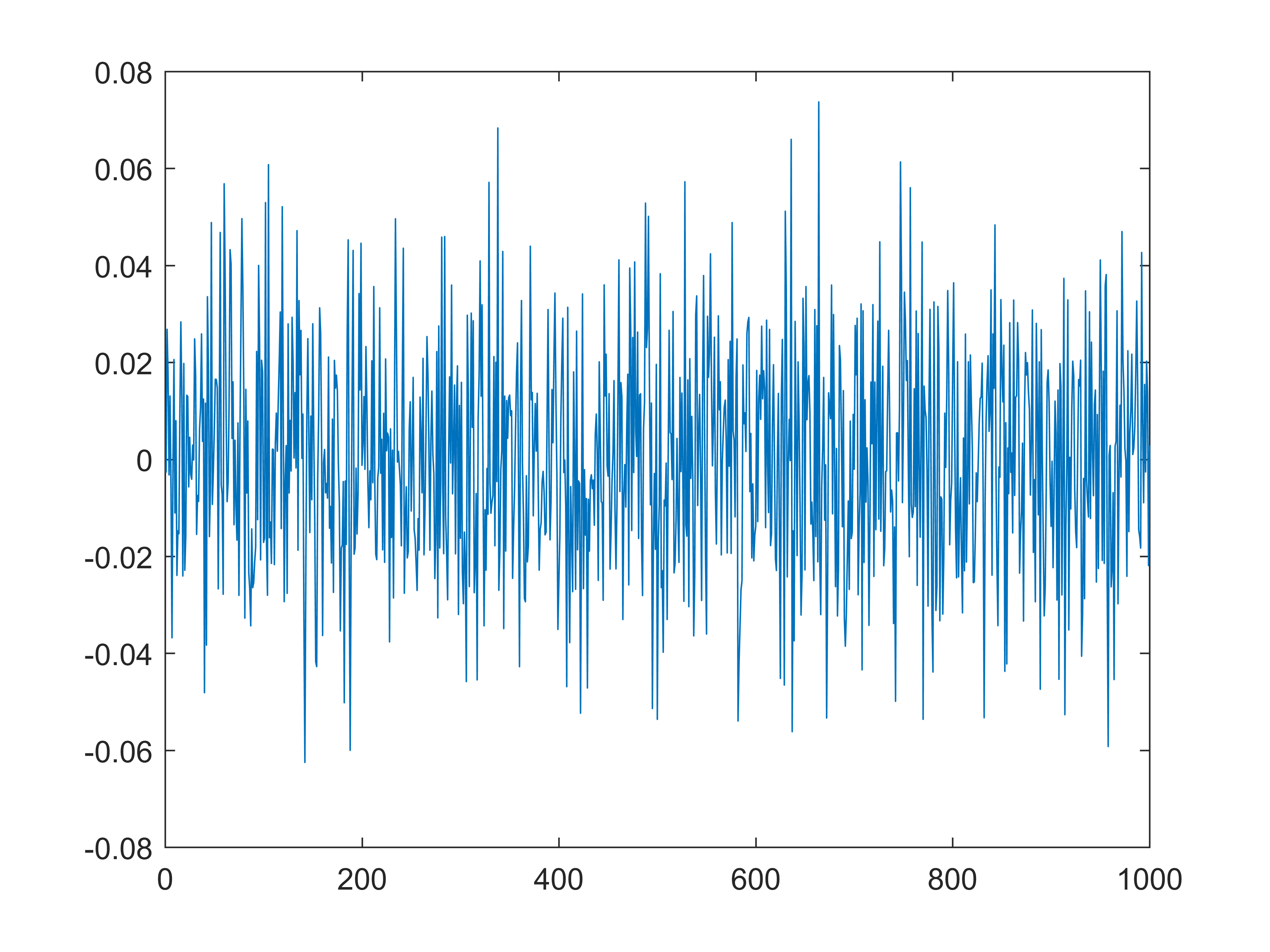Fig 1. 白噪声频谱的时域波形

2. GCC-PHAT的理论推导

首先，应当明确“使用GCC-PHAT来计算时延”的出发点如下：

  1. 传统的时域互相关法，计算量较大且运算时间慢。
  2. 使用频域法来计算互相关（CC）十分经典，但是不能满足更高的要求。
  3. 在频域法CC的基础上，对互功率进行“系数加权”，由此产生了一系列的广义互相关法（GCC）。
  4. 在GCC中，控制加权函数以进行相位加权可以对输出结果进行锐化，这便是GCC-PHAT。
  5. GCC-PHAT常与SRP-PHAT结合并应用到目标定位中去。

2.1 频域法CC

先分析经典的频域法求解CC，首先对信号进行建模，这里直接考虑的是含噪模型，目标发射信号 ${ x\left( t \right)}$ ，两路接收信号分别为：
$$
{x_1}\left( t \right) = x\left( {t - {t_1} } \right) + {n_1}\left( t \right) \tag{1}
$$

$$
{x_2}\left( t \right) = x\left( {t - {t_2}} \right) + {n_2}\left( t \right) \tag{2}
$$

为了表达方便，其实可以将第一路信号 ${ x_1\left( t \right)}$ 作为参考信号，直接将第二路信号表示为：

$$
{x_2}\left( t \right) = x_1 \left( {t - {t_0}} \right) + {n_0}\left( t \right) \tag{3}
$$

经典的频域法求解流程是：对两路信号分别进行傅里叶变换，计算互功率，最终反变换到时域。由傅里叶变换可得，两路信号在频域之间的关系为：
$$
{X_2}\left( \omega \right) = {X_1}\left( \omega \right) \cdot {e^{ - j\omega {t_0}}} + {N_0}\left( \omega \right) \tag{4}
$$

两路信号的互功率为：

$$
P\left( \omega \right) = {X_1}\left( \omega \right) \cdot X_2^*\left( \omega \right) \tag{5}
$$

此时为了表达方便，将第一路信号的频谱表示为幅值和相位的形式：
$$
{X_1}\left( \omega \right) = A\left( \omega \right) \cdot {e^{jB\left( \omega \right)} } \tag{6}
$$
由此可得互功率的表达形式为：
$$
\begin{align}
P\left( \omega \right)
& = A\left( \omega \right) \cdot {e^{jB\left( \omega \right)}} \cdot {\left[ {A\left( \omega \right) \cdot {e^{jB\left( \omega \right)}} \cdot {e^{ - j\omega {t_0}}} + {N_0}\left( \omega \right)} \right]^*} \cr
& = {\left| {A\left( \omega \right)} \right|^2} \cdot {e^{j\omega {t_0}}} + A\left( \omega \right) \cdot {e^{jB\left( \omega \right)}} \cdot N_0^*\left( \omega \right)
\end{align}
\tag{7}
$$
可以看到，上式共有两部分构成，第一部分是 ${ x_1\left( t \right)}$ 和 ${ x_1\left( t-t_0 \right)}$ 的互功率，第二部分是 ${ x_1\left( t \right)}$ 和噪声 ${ n_0\left( t \right)}$ 的互功率，利用傅里叶变换可以得到对应的时域输出为：
$$
p\left( t \right) = {R_{ {x_1}{x_1} } }\left( \tau \right)*\delta \left( {t - {t_0} } \right) + {R_{ {x_1}{n_0} } }\left( \tau \right) \tag{8}
$$
对（7）式也可以理解为：互功率中主要有两部分构成，一部分是期望的功率与 ${exp(jwt_0)}$ 的相乘，这里是最为关键的部分，因为这个线性相位最终决定了输出冲激的位置。而第二部分是参考信号与信号之间的互功率，一般认为二者之间的相关性很小，因此这一部分直接忽略不计。但是随着噪声的不断增加，第二部分对最终结果的干扰也会越来越强。

2.2 GCC-PHAT

这里在频域法CC的基础上，先来考虑理想无噪情况下的GCC-PHAT，此时（7）和（8）式中的互功率以及时域中的互相关函数将转换为以下更为简单的形式：
$$
P\left( \omega \right) = {\left| {A\left( \omega \right)} \right|^2} \cdot {e^{j\omega {t_0} } } \tag{9}
$$

$$
p\left( t \right) = {R_{ {x_1}{x_1} } }\left( \tau \right)*\delta \left( {t - {t_0} } \right) \tag{10}
$$

可以发现，最终时域的结果是在准确时延 ${t_0}$ 处的冲激与信号 ${x_1(t)}$ 的自相关之间的卷积。而信号的自相关是以0时延为轴对称分布的，且在0时延周围呈现类似 ${sinc}$ 函数的形式，因此二者的卷积必然导致将自相关函数搬移至 ${t_0}$ 处。也可以理解为，信号的自相关导致在准确时延 ${t_0}$ 处的冲激变得“发散”了。

因此，一种十分直接了当的，用来抑制这种发散或者说“锐化”结果的思路就是，在频域对幅值进行归一化，也就是进行以下处理（使用matlab代码形式简单表示）：

1
2
3
4
% 幅值归一化
p(w) = p(w)./abs(p(w));
% 或者直接取相位
p(w) = angle(p(w));

这种操作被称为PHAT（PHAse Transform），也可以归纳为对于互功率的“加权”，属于GCC的一种。可以预见到进行PHAT加权后结果将变得十分尖锐（趋向于理想的冲激函数）。

然而对于实际中含噪的情况，结果却不是十分乐观，这里仍把（7）式摘录如下：
$$
P\left( \omega \right) = {\left| {A\left( \omega \right)} \right|^2} \cdot {e^{j\omega {t_0} } } + A\left( \omega \right) \cdot {e^{jB\left( \omega \right)} } \cdot N_0^*\left( \omega \right) \tag{7}
$$
可以发现此时进行幅值归一化的时候，并不能完整的消除 ${ {\left| {A\left( \omega \right)} \right|^2} }$，这是由于增加的噪声项所致。并且随着噪声的增大，归一化的结果反而会越来越差。这一点可以从取相位的角度来分析，可以发现最终的结果是由两项相加得到的，并且不能表示为因子连乘的形式，而对于两个复数相加最终取相位的形式，可以见下图：

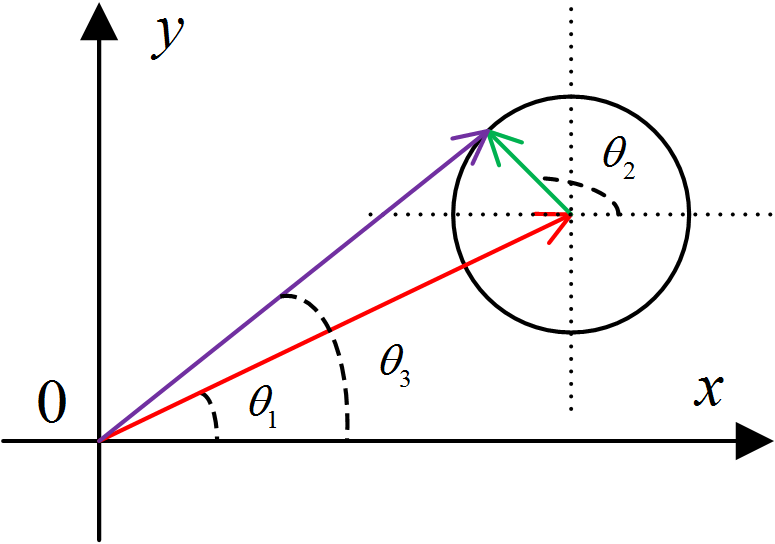Fig 2. 两复数相加结果取相位

可以发现，最终的相位实际上与二者的幅值有很大的关系，当二者的幅值相差加大时，幅值较大的复数的相位占据了主要地位；即便是幅值较小复数的相位可以任意选取，但是对最终和的相位的影响却十分微小。

因此对于含噪情况下的GCC-PHAT，从取相位的角度进行分析可得：

  • 当噪声很小时，使用GCC-PHAT可以获得较为准确的结果，并且结果十分尖锐
  • 随着噪声的增大，噪声的相位占据了主要成分，GCC-PHAT的结果越来越不准确，结果中出现了大量混杂的噪声成分。

因此，综上对比经典的频域法CC以及GCC-PHAT法，可以进行一番小结：

  • 后者通过丢弃频域幅度的信息，可以获得时域上十分尖锐的结果，但是抗噪性能大为减弱。
  • 前者完全保留了频域幅度的信息，导致结果出现了一定的发散，但是抗噪性能优良。

从原理上分析，其它类型的GCC都是在此基础上选取了各式各样的加权系数，目的都是通过尝试来舍弃或保留一定的时频信息，来实现特定的目的和结果。

3. 仿真结果

以下是利用实测信号求解时延的仿真结果，其中各个参数以及信号建模的流程如下：

  • 原始信号由手机录音采集，采样率为 ${fs = 48000 Hz}$。

  • 并且截取了约 ${20 ms}$ 的片段（1000点，作为语音信号处理中的一帧）作为参考信号 ${x_1}$。

  • 之后直接对 ${x_1}$ 进行时延处理作为理想的 ${x_2}$ 信号，即 ${x_2\_ideal}$，时延大小为 ${delay = 5.123e-4s}$ 。

  • 对 ${x_2\_ideal}$ 进行人工加噪作为实际的 ${x_2}$ 信号，即 ${x_2\_pract}$。

以下分别使用CC频域法以及GCC-PHAT的方法进行求解时延，代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
%% 初始化
clear;
clc;
close all;

% 读取原始数据
load('data.mat', 'testData');                 % 也可以采用其他的数据

% 设置参数
fs    = 48000;
delay = 5.123e-4;
snr   = 40;

% 三路信号
x1       = testData(4e4:4.0999e4);   		   % 这里是为了刚好取到1000点
x2_ideal = delayseq(x1, delay, fs);
x2_pract = awgn(x2_ideal, snr);

% 计算滤波器前的互相关
xcorr11_gcc       = my_gcc_phat(x1, x1);
xcorr12_ideal_gcc = my_gcc_phat(x2_ideal, x1); % 这里看的是x2_ideal相对x1的时延
xcorr12_pract_gcc = my_gcc_phat(x2_pract, x1);
xcorr11_cc        = xcorr(x1, x1);
xcorr12_ideal_cc  = xcorr(x2_ideal, x1);       % 这里看的是x2_ideal相对x1的时延
xcorr12_pract_cc  = xcorr(x2_pract, x1);

% 作图
figure(1);
subplot(311);plot(x1);      title('参考信号x1');          axis tight;grid on;
subplot(312);plot(x2_ideal);title('理想时延信号x2\_ideal');axis tight;grid on;
subplot(313);plot(x2_pract);title('含噪时延信号x2\_pract');axis tight;grid on;

figure(2);
subplot(321);plot(xcorr11_cc);       title('参考信号x1');          axis tight;grid on;
subplot(323);plot(xcorr12_ideal_cc); title('理想时延信号x2\_ideal');axis tight;grid on;
subplot(325);plot(xcorr12_pract_cc); title('含噪时延信号x2\_pract');axis tight;grid on;
subplot(322);plot(xcorr11_gcc);      title('xcorr11\_gcc');       axis tight;grid on;
subplot(324);plot(xcorr12_ideal_gcc);title('xcorr12\_ideal\_gcc');axis tight;grid on;
subplot(326);plot(xcorr12_pract_gcc);title('xcorr12\_pract\_gcc');axis tight;grid on;

结果如下所示：

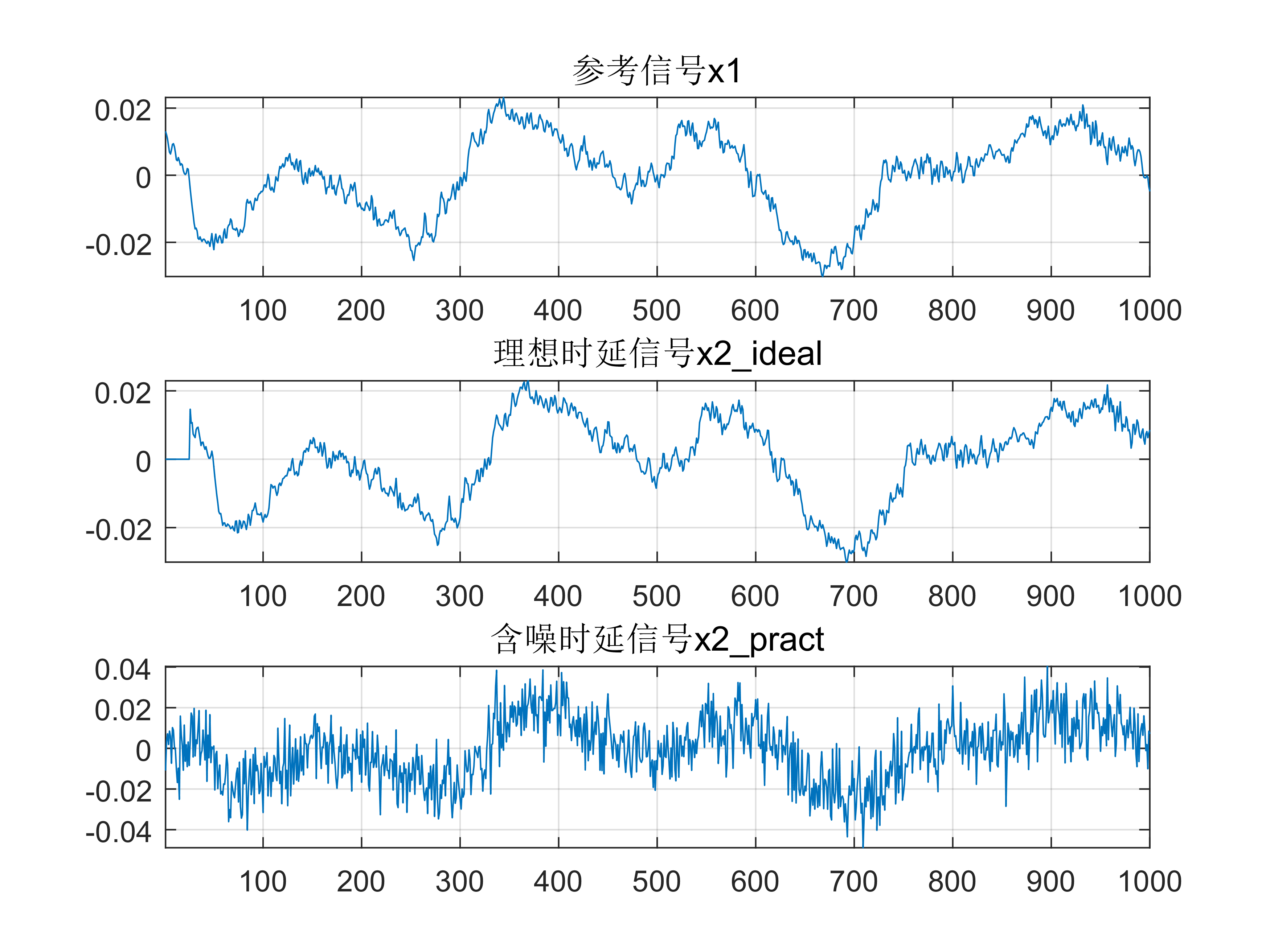Fig 3. 信号建模

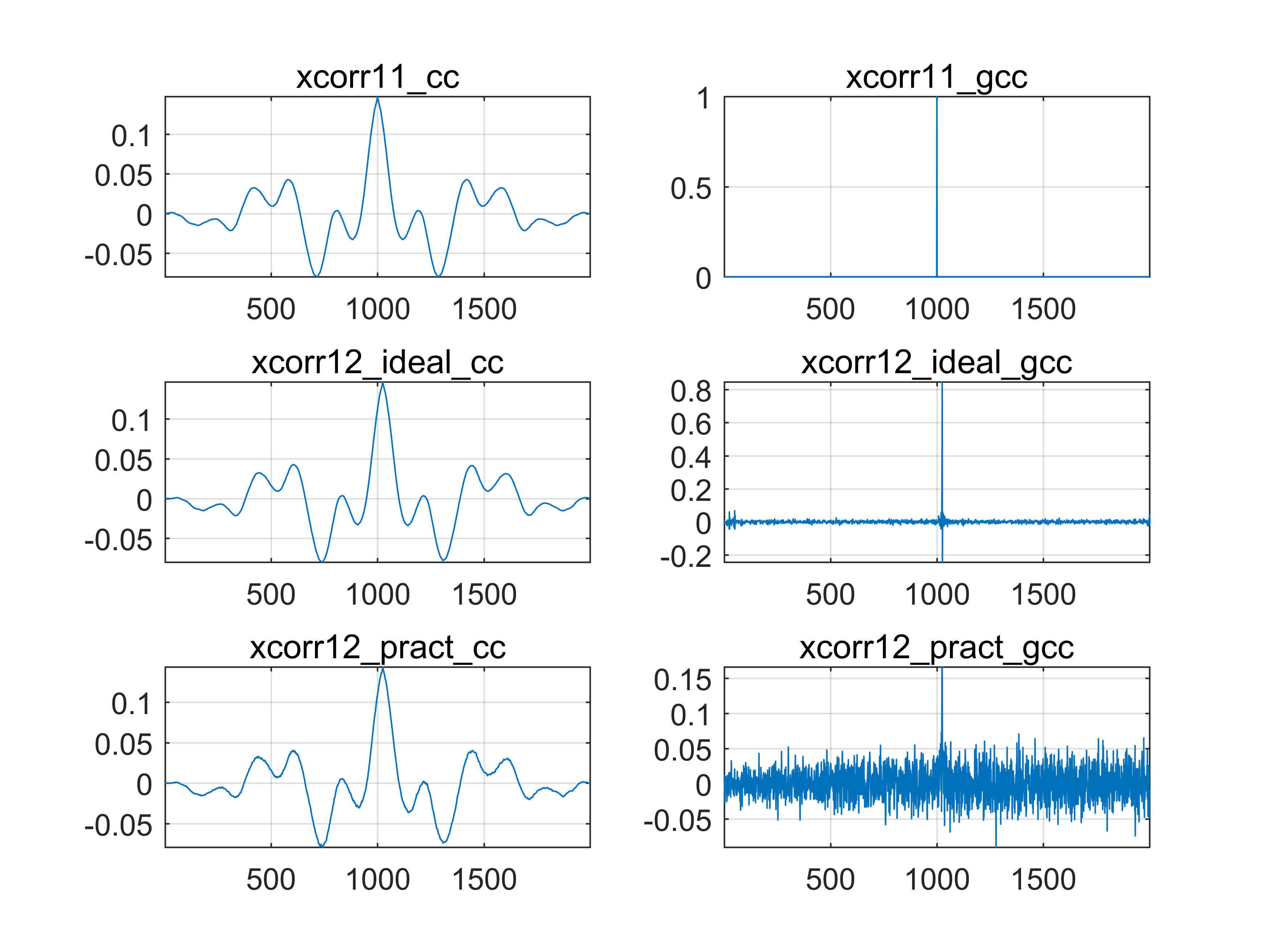Fig 4. 使用不同方法进行时延估计

说明：

标题中的结尾后缀表示了使用的方法，cc（频域法）、gcc（GCC-PHAT）。中间的数字以及第二个下化线表示了进行互相关的两路信号，如 xcorr12_pract_gcc 表示使用 GCC-PHAT 的方法对信号 x1 与 x2_pract 进行时延估计；而 xcorr11_cc 表示使用频域法对信号 x1 和 x1 进行时延估计，也就是 x1 的自相关。

可以发现理想情况下（SNR为40dB），GCC-PHAT的效果十分优异。以下将信噪比设置为20dB，并观察结果的放大图：

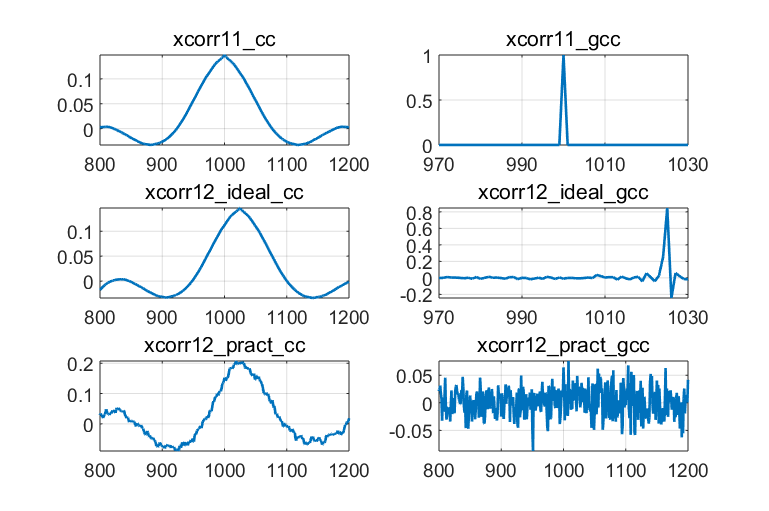Fig 5. 低信噪比下的时延估计

可以发现传统的（频域）CC可以取得不错的效果，即便是在低信噪比的恶劣条件下，依然可以表现出一定的时延估计能力，但是缺点在于结果较为“发散”。而GCC在高信噪比下获得了十分尖锐的结果，但是噪声功率一旦过大，则结果迅速恶化。即随着噪声功率的增加，GCC-PHAT的性能逐渐下降，这些与理论分析都是一致的。

4. 时延精度与采样率

上面的仿真只是从更加贴近实际应用的角度出发，验证了对于GCC-PHAT的理论分析。但是在实际的估计时延的场景中，需要面对的一个问题就是时域结果的精度。

注意到在仿真中，时延参数为 ：${delay = 5.123e-4s}$（一看就知道是随便设置的），因此对应的时延点数为：${points = fs * delay = 24.5904}$ 。但是实际中的点数不可能出现小数形式，因此这里必然存在由采样而引入的估计误差。那么如何获取准确的时延点数或者提高时延估计的精度呢？

这里以理想的不含有噪声的情况为例：

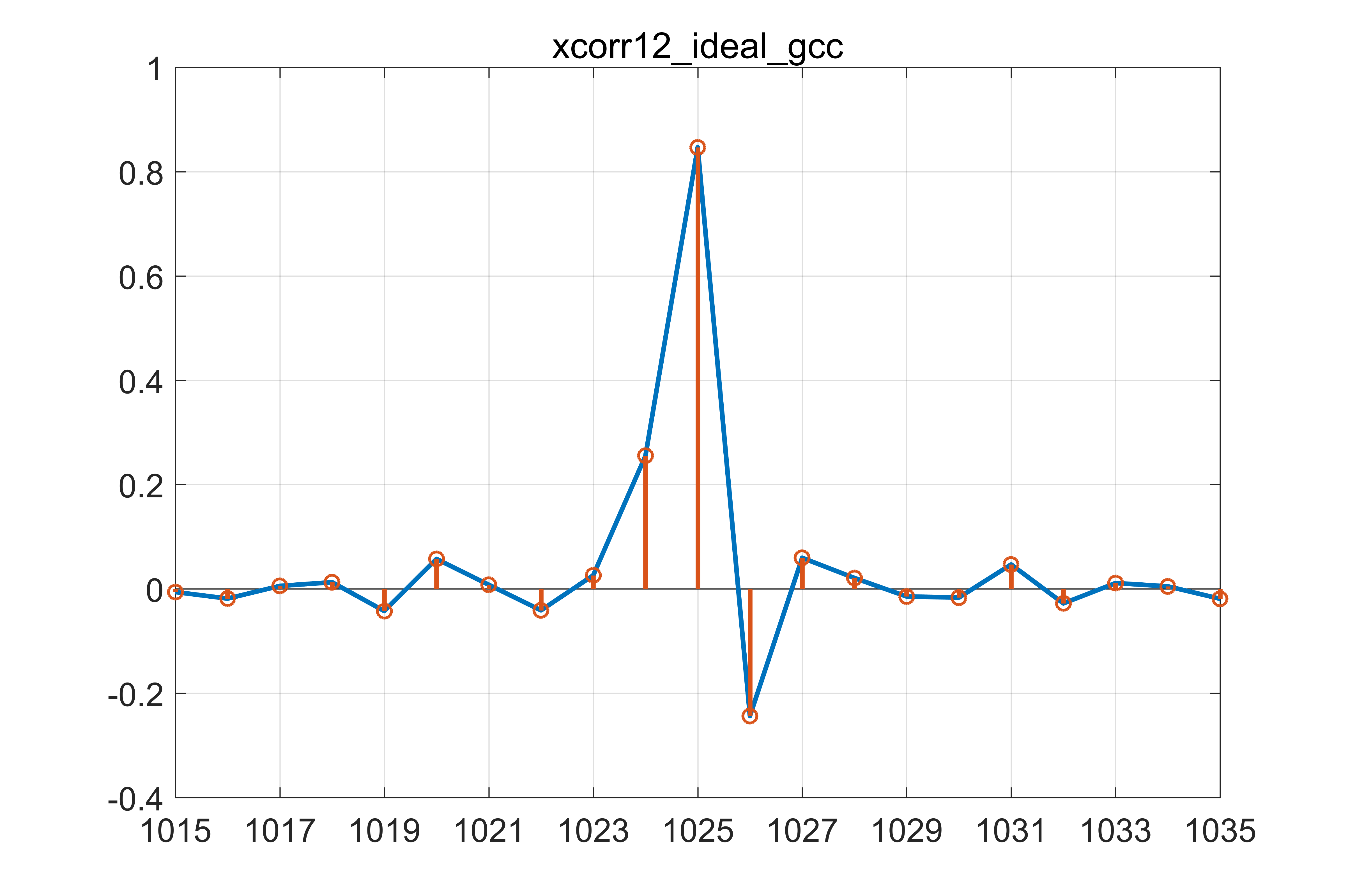Fig 6. 理想无噪情况下的结果

可以很直观的看到，利用GCC-PHAT得到的结果为：${points = 25}$，与准确的 24 点时延存在一定的误差。可以发现这个误差完全是由于采样率 ${fs = 4800Hz}$ 所制约，也就是说要想提高最终的估计结果的精度，只有提高麦克风对于原始信号 ${x_1}$ 以及 ${x_2}$ 的采样率？

一开始我陷入了这里的误区，但是后来考虑到对于人类语音而言，采样率 ${fs = 48000Hz}$ 完全是绰绰有余的，那么问题出现在哪呢？原始是我没有理解采样以及时域和频域的关系。我之前总是使用一种固有的眼光去看的采样，总觉得时域采样，使得可以表现出来的信号点数减少了，因此导致了精度的下降。事实上，并不能认为是采样导致了信息丢失，而是信心通过采样转换为了频域的形式。也就是说，根据奈奎斯特采样定理，使用 ${fs = 480Hz00}$ 可以无损的恢复出 ${[0, 24000Hz]}$ 内的成分。

因此考虑到时域采样以及频域周期延拓的对应关系，那么恢复出原始波形的步骤是频域加窗，也就是等价于时域卷积 ${sinc}$ 函数，因此可以使用时域 ${sinc}$ 插值在一定程度上恢复出原来的信号。

插值后的结果如下：

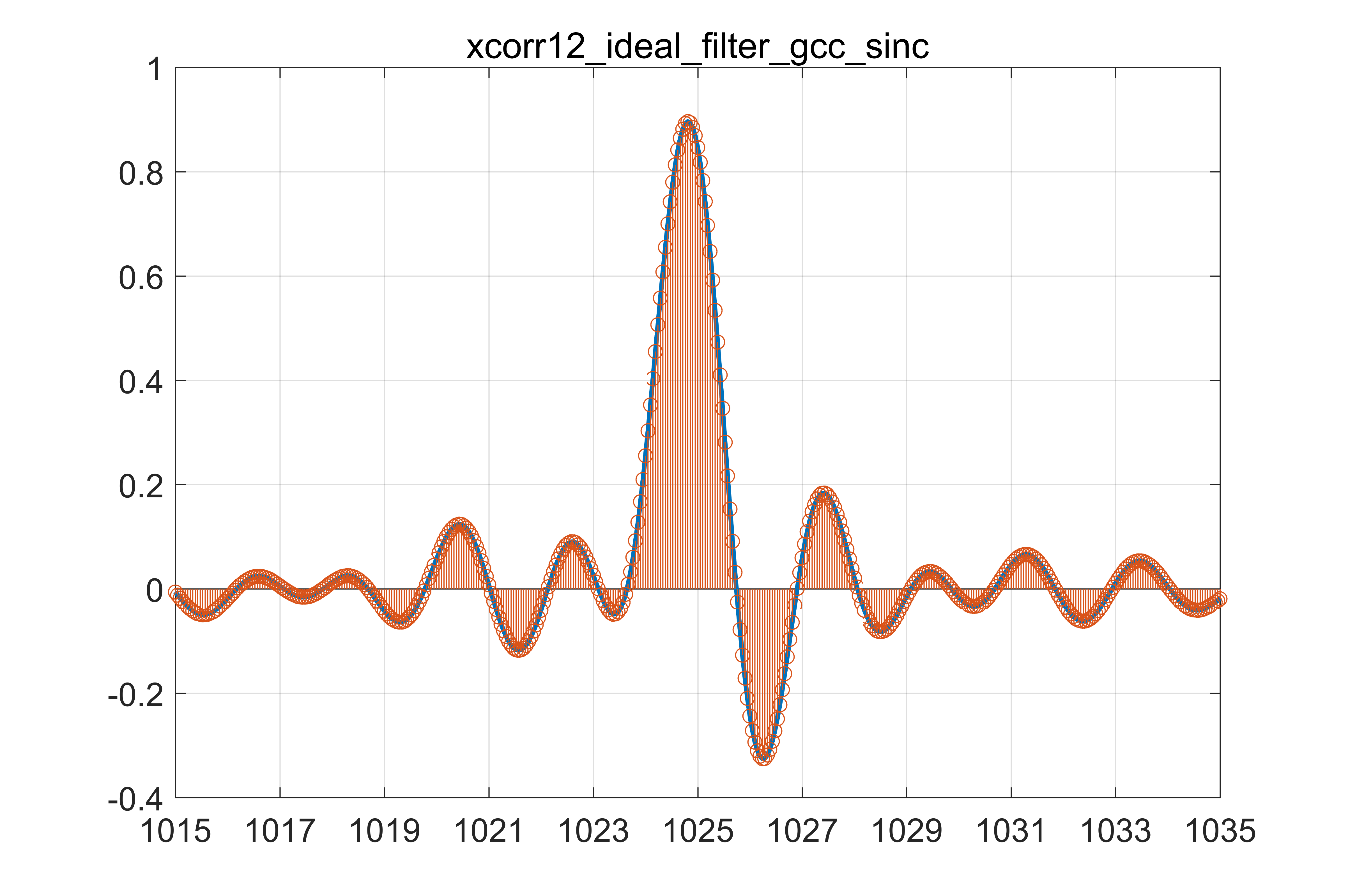Fig 7. sinc插值后结果

其中相邻两点之间新插值点数为20，最终的结果约为24.75，可以看到与24.59十分接近。但是仍然存在一定误差，分析如下：

  • 选择的插值原始数据不是无限长的。
  • 由于FFT的原因，导致原始的无限长的数据发生了搬移和叠加，因此必然发生了混叠，导致结果不准确。
  • 但是这个精度对于很多场景已经足够 了。

其中使用到的插值函数如下所示，由我本人所写的（可能存在bug）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
function [y, m] = my_sinc_vector(x, n, num)
% Note:
%       This function is used to realize 'Sinc interpolation'.
% Usage:
%       [y, n] = my_sinc_vector(x, n, number)
% Input arguments:
%       x   : the original signal (1*N)
%       n   : the original time axis (1*N)
%       num : the number of interpolation points between two original points.
% Output arguments:
%       y   : the output signal (about 1*N*number)
%       m   : the output time axis (about 1*N*number)
% For example:
%       x   = sin(1:10);
%       n   = 1:10;
%       num = 5;
%       [y, m] = my_sinc_vector(x, n, num);
%       plot(n,x,'-o','linewidth',2);
%       hold on;
%       stem(m,y);
% 说明：
%       本函数用来实现sinc插值
%       输入：原始信号，原始信号对应时间轴（点数），原始两点之间新插入的点数
%       输出：插值后信号，插值后时间轴
%       注意：这个函数返回的是一组向量（包括信号向量、时间向量）

% --------------------------------------------------------------
% 初始化
N = length(n)+num*(length(n)-1); % 总点数
y = zeros(1,N);                  % 输出信号矢量
m = zeros(1,N);                  % 输出时间矢量

% --------------------------------------------------------------
% 进行插值
for ii = 1:N
    if(mod(ii,num+1)==1)                  % 如果刚好取到
        y(ii) = x(ceil(ii/(num+1)));
        m(ii) = n(ceil(ii/(num+1)));
    else                                  % 如果没有取到
        y_cac = 0;                        % 累加变量
        m_before = n(ceil(ii/(num+1)));   % 当前插值点之前的原始时间位置
        m_back = n(ceil(ii/(num+1))+1);   % 当前插值点之后的原始时间位置
        dt = (m_back-m_before)/(num+1);   % 该插值区间的分辨率
        m_cac = m_before+dt*(ii-(num+1)*(ceil(ii/(num+1)-1))-1); % 新插值点对应的时间位置
        for jj = 1:length(n)
            y_cac = y_cac + x(jj)*sin((m_cac-n(jj))*pi)/((m_cac-n(jj))*pi); % 进行sinc插值累加
        end
        y(ii) = y_cac; % 信号赋值
        m(ii) = m_cac; % 时间赋值
    end
end

end

5. 降噪引发的思考

上一小节展示的是理想无噪的情况，一方面增加采样率可以增加时延估计的精度。但是在含噪情况下如何增加精度？可以看到GCC-PHAT对于噪声是十分敏感的。

这里我尝试使用了最为简单的滤波，即对信号进行带通滤波。可以看到即使是作为理想参考信号的 ${x_1}$，本身也是带有噪声的。考虑到在本文中使用的信号都是是人类的语音信号，因此可以利用先验知识，进行 ${[50Hz, 3400Hz]}$ 的频带滤波。这种方式可以在一定程度上提高信噪比，但是始终应当明确这种预滤波不能破坏两路信号之间的时延关系，否则滤波便失去了意义。

经过理论推导可以发现，无论是FIR（线性相位）还是IIR（非线性相位），滤波都不会影响相对时延关系，因为最终的互功率的表达式都会转换为：

$$
\begin{align}
P\left( \omega \right)
& = \left[ A\left( \omega \right) \cdot e^{jB\left( \omega \right)} \cdot H\left( \omega \right) \right] \cdot \left[ {H\left( \omega \right) \cdot \left[ {A\left( \omega \right) \cdot {e^{jB\left( \omega \right)} } \cdot {e^{ - j\omega {t_0} } } + {N_0}\left( \omega \right)} \right] } \right]^* \cr
& = {\left| {H\left( \omega \right)} \right|^2} \cdot \left[ { { {\left| {A\left( \omega \right)} \right|}^2} \cdot {e^{j\omega {t_0} } } + A\left( \omega \right) \cdot {e^{jB\left( \omega \right) } } \cdot N_0^*\left( \omega \right)} \right]
\tag{7}
\end{align}
$$

可以看到，滤波器只是贡献了幅度因子。因此即便是滤波器本身不满足线性相位，最终也不会影响结果，但是前提是保证对两路信号进行了完全一致的处理。

以下使用代码仿真如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
% 预滤波之后的结果
x1_filter       = my_prefilter(x1, 50, 3400, fs); 
x2_ideal_filter = my_prefilter(x2_ideal, 50, 3400, fs); 
x2_pract_filter = my_prefilter(x2_pract, 50, 3400, fs); 

% 计算滤波器后的互相关
xcorr11_filter_gcc       = my_gcc_phat(x1_filter, x1_filter);
xcorr12_ideal_filter_gcc = my_gcc_phat(x2_ideal_filter, x1_filter);
xcorr12_pract_filter_gcc = my_gcc_phat(x2_pract_filter, x1_filter);
xcorr11_filter_cc        = xcorr(x1_filter, x1_filter);
xcorr12_ideal_filter_cc  = xcorr(x2_ideal_filter, x1_filter);
xcorr12_pract_filter_cc  = xcorr(x2_pract_filter, x1_filter);

figure(3);
subplot(311);plot(x1_filter);      title('x1\_filter');       axis tight;grid on;
subplot(312);plot(x2_ideal_filter);title('x2\_ideal\_filter');axis tight;grid on;
subplot(313);plot(x2_pract_filter);title('x2\_pract\_filter');axis tight;grid on;

figure(4);
subplot(321);plot(xcorr11_filter_cc);
title('xcorr11\_filter\_cc');        axis tight;grid on;
subplot(323);plot(xcorr12_ideal_filter_cc);
title('xcorr12\_ideal\_filter\_cc'); axis tight;grid on;
subplot(325);plot(xcorr12_pract_filter_cc);
title('xcorr12\_pract\_filter\_cc'); axis tight;grid on;
subplot(322);plot(xcorr11_filter_gcc);
title('xcorr11\_filter\_gcc');       axis tight;grid on;
subplot(324);plot(xcorr12_ideal_filter_gcc);
title('xcorr12\_ideal\_filter\_gcc');axis tight;grid on;
subplot(326);plot(xcorr12_pract_filter_gcc);
title('xcorr12\_pract\_filter\_gcc');axis tight;grid on;

其中my_prefilter是自己编写的预滤波的函数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function y = prefilter(x, lowfre, highfre, fs)
% Note:
%       This function is used to do the 'prefilter', a bandpass filter.
% Usage:
%       y = prefilter(x, lowfre, highfre, fs)
% Input arguments:
%       x       : the input signal (1*N)
%       lowfre  : the lower frequency
%       highfre : the high frequency
%       fs      : the sampling frequency
% Output arguments:
%       y       : the output signal
% For example:
%       x       = randn(1,2000);
%       lowfre  = 50;
%       highfre = 3400;
%       fs      = 48000;
%       y       = %%%;
% 说明：
%       本函数用来实现预滤波（带通滤波）
%       输入：原始信号，低频门限，高频门限，采样率
%       输出：滤波后信号

% --------------------------------------------------------------
% 设计带通滤波器
filterd=fdesign.highpass('N,Fc',50,lowfre,fs);  % 50阶的高通滤波器
filterd2=fdesign.lowpass('N,Fc',50,highfre,fs); % 50阶的低通滤波器
Hd=design(filterd);
Hd2=design(filterd2);

% --------------------------------------------------------------
% 进行滤波
y = filter(Hd,x);  % 高通滤波
y = filter(Hd2,x); % 低通滤波    

end

结果如下：

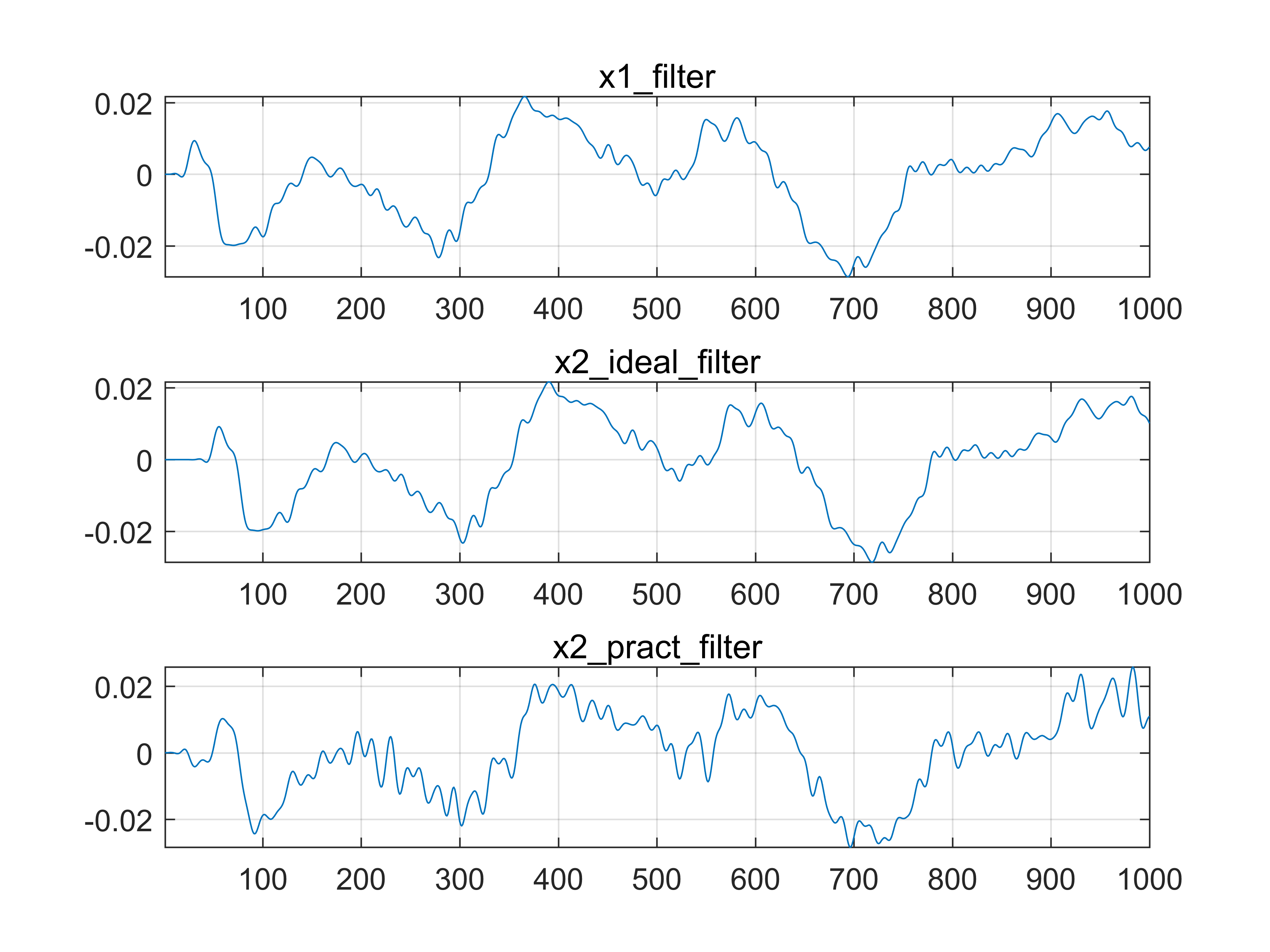Fig 8. 预滤波结果

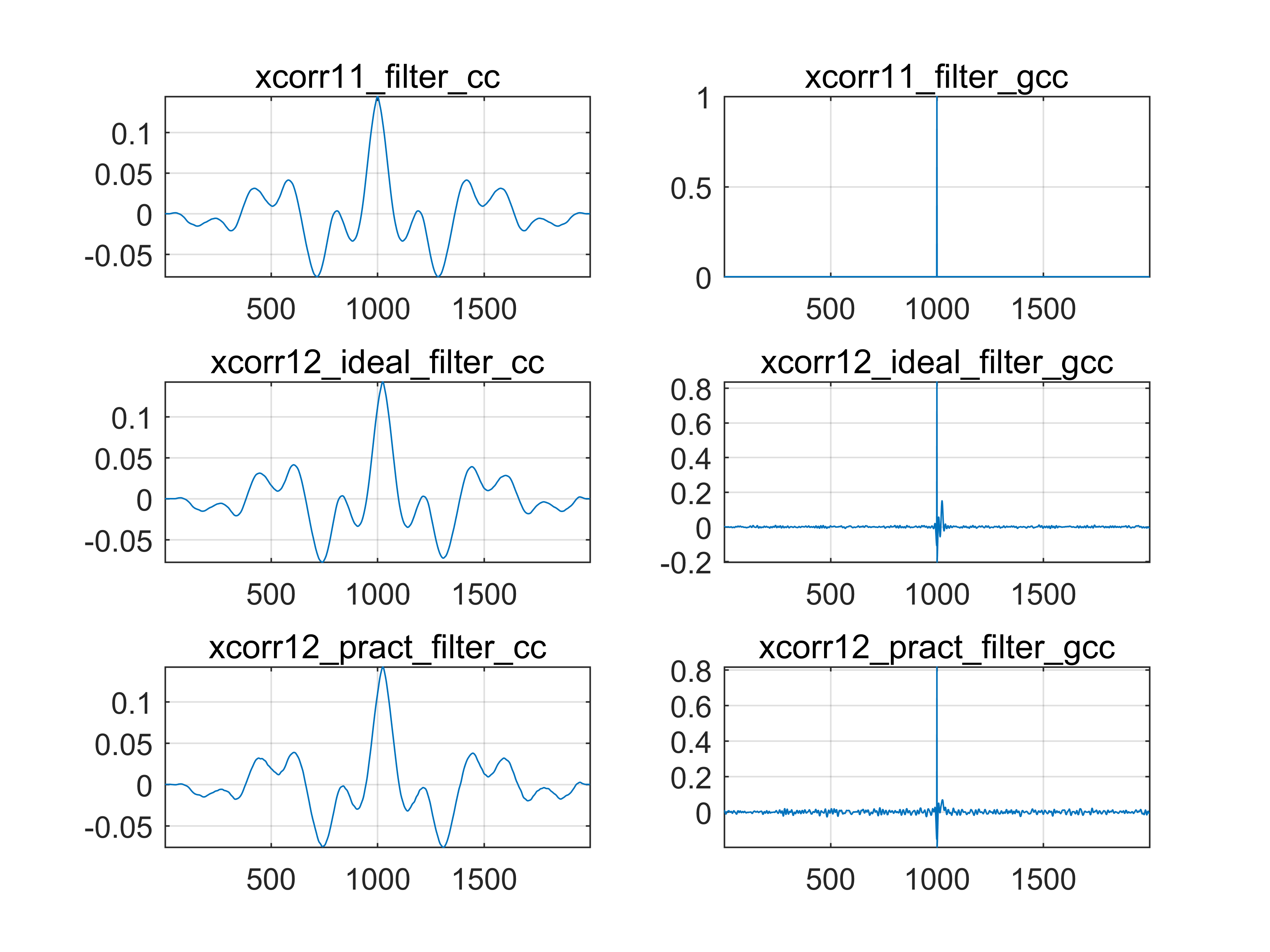Fig 9. 预滤波后使用不同方法进行时延估计

注意这里的信噪比设置为40dB，可以发现使用GCC-PHAT处理滤波后的信号时出现了一个问题，即在0时延处出现了较大的冲激（在期望的时延处仍有较小的峰值），这显然不是正确的结果。

这个问题困扰了我很长时间，也正是由于此我才推迟了写这篇文章的时间，我花费了很长的时间思考后从两个角度分析了一下：

  • 从理论上讲，滤波器只是贡献了幅度因子，因为即便是滤波器本身不满足线性相位，最终也不会影响结果，但是前提是保证对两路信号进行了完全一致的处理。因此发生这种情况可能是因为两路信号没有使用完全一致的滤波器所致，因此我准确去查看filter函数的源代码。可惜，查看不了，这是内置的函数。应该是由其它更底层的语言所写，属于matlab的核心知识产权，所以这只能成为一种猜想。
  • 从实践上讲，我查看了一下互功率结果的相位，结果发现有点意思：

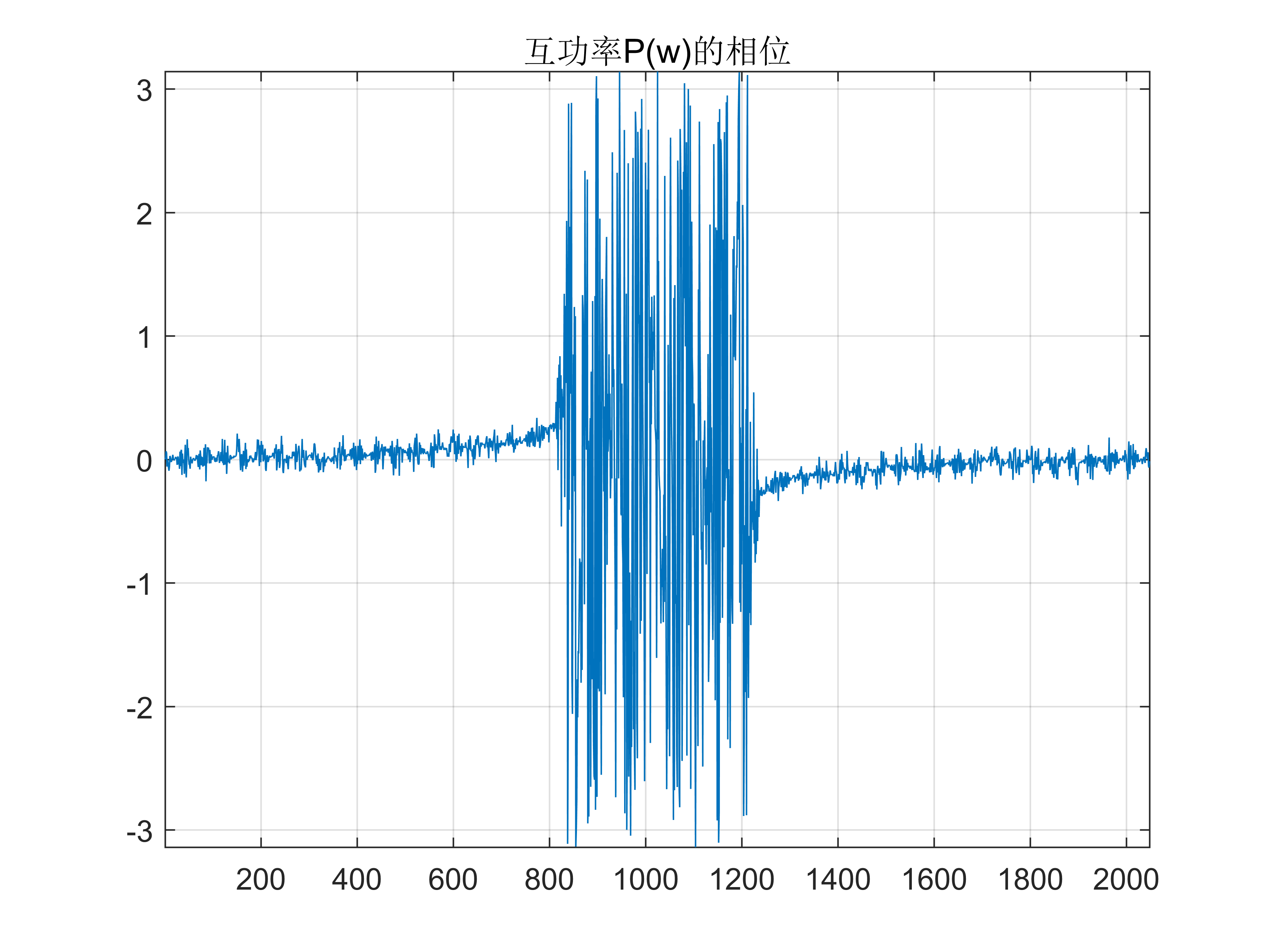Fig 10. 互功率的相位

注意横轴没有进行处理，但是事实上这里的横轴指的是 ${[-fs/2, fs/2]}$。可以看到，互功率只保留了 ${[50Hz, 3400Hz]}$ 频带内的成分。从另外一种角度分析，考虑时域和频域的对偶性，如果将上图看做一个时域信号，则发现其存在一个较强的直流成分，因此在频域会有一个很大的零频分量。因此上图（频域中的互功率）对应的傅里叶变换，即时域中的互相关的结果，会在0时延处产生一个较大的冲激。

其实分析这个冲激产生的原因：应该是对于滤波的方法没有进行深刻理解。其实从式（7）式就可以看到，当两路信号的滤波处理，完全保持一致的时候，最终的滤波处理只是在互功率上进行了线性处理，因此对于相位完全没有影响，而且对于幅度也完全没有影响。

其实，出发点是利用信号主要聚集在 ${[50Hz, 3400Hz]}$，带通滤波后可以增强信号的成分，减弱信号。因此滤波后，在进行后续的GCC-PHAT处理前，必须对互功率进行加窗处理，即只使用 ${[50Hz, 3400Hz]}$ 频带内的信息，而非整个频带的信息，否则就失去了意义。

以下人工取横轴区间为 ${[824, 1224]}$ 进行测试（总FFT点数为2048，保持对于中心1024的对称），可以发现结果为：

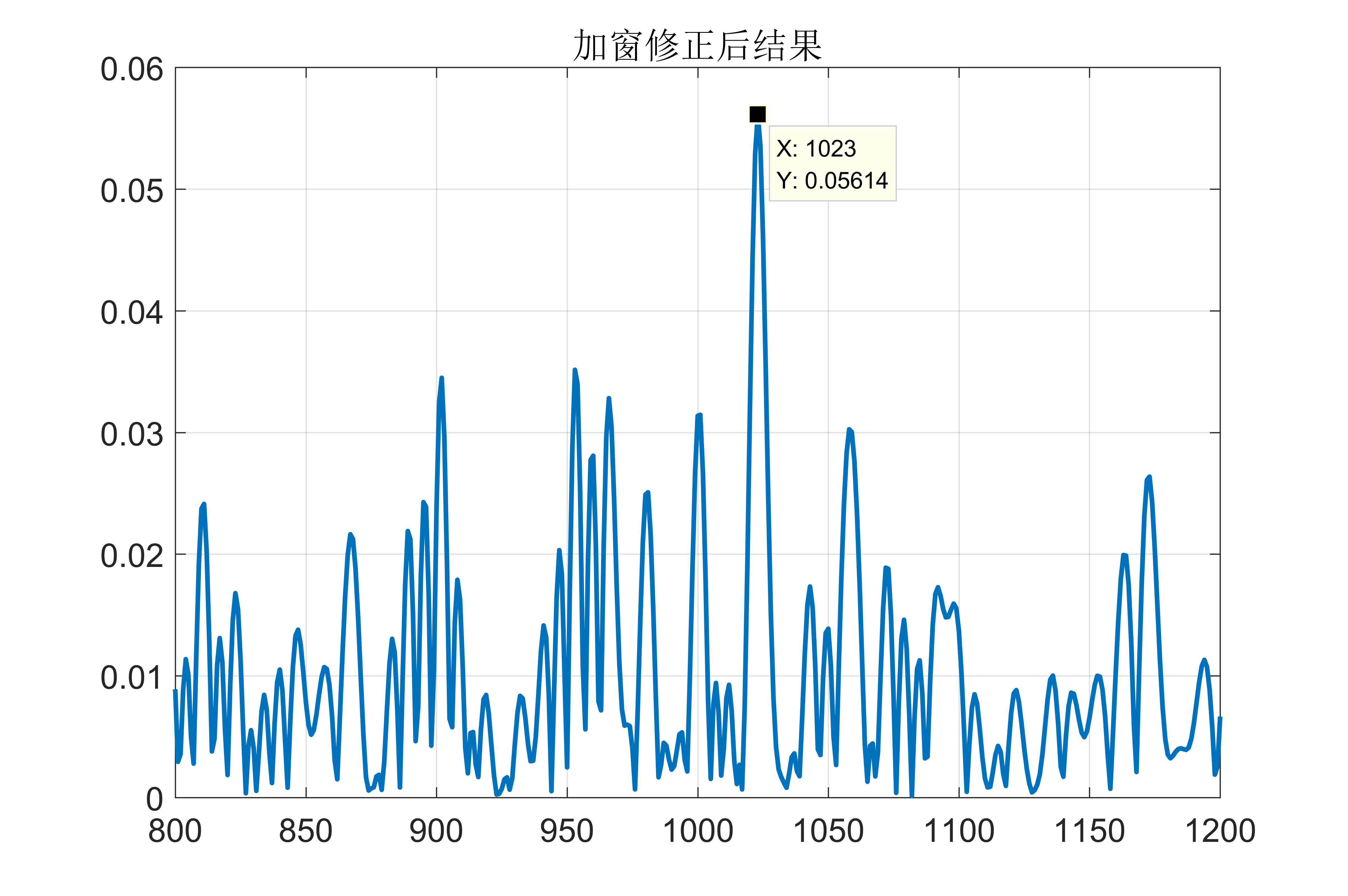Fig 11. 预滤波并且加窗处理后的结果

可以看到结果显示为1023点，利用 ${sinc}$ 插值可以将结果进一步确定为 ${[1023, 1024]}$ 之间，基本处于正确的结果附近。但是无法再进一步增加精度了，这是由信噪比所限制的。

6. 总结

综上所述，对比经典的频域法CC以及GCC-PHAT可以发现：

  • 后者通过丢弃频域幅度的信息，可以获得时域上十分尖锐的结果，但是抗噪性能大为减弱。
  • 前者完全保留了频域幅度的信息，可以获得优良的抗噪性能，但是幅度信息导致了结果出现发散。

其它的GCC都是在此基础上提出了各式各样的加权系数，目的都是通过选取不同程度的时频信息，来实现特定的目的和结果。

而在工程的层面上，提高最终时域估计精度的方式有：

  • 使用 ${sinc}$ 插值可以使结果复原，但是这属于“扬汤止沸”的方式。
  • 增大SNR可以提高精度，这属于“釜底抽薪”的方式。

因此可以看到，使用GCC-PHAT来求解信号的时延，最重要的因素还是SNR。还有一个问题值得强调：

问：当SNR很高时，GCC-PHAT和直接频域法求互相关都可以获得信号的准确时延，那么GCC-PHAT方法的优势在于哪些地方？

答：在于结果十分尖锐，很多时候我们目的并不只是为了求解准确的时延。有可能在某次处理中返回了一个在准确时延附近的值，我们需要一个系数来表示该点与准确值的误差程度，而传统的互相关结果是发散的，导致对于误差不是很敏感。而对于GCC-PHAY锐化后的结果，对误差则十分敏感。稍有误差，则会赋予一个十分小的权重，因此这是GCC-PHAT的优势所在。

7. 后记

写这种技术文档真是太麻烦了，我原以为一上午就能弄完，结果陆陆续续拖了2天时间，不仅仅是公式和图的修改，更关键的是在写的过程中总能发现一些错误，这样遇到问题就会停下来拖慢了进度。。。

这篇文章是上一篇文章的的续篇，但是我加了一些仿真时遇到的问题和思考，导致篇幅有些多，能完整看下来的都是同行啊哈哈。希望以这一篇作为对信号时延估计的小收尾，文中有什么纰漏欢迎指出并与我联系。

-------------本文结束感谢您的阅读-------------